Introduction

DeepSeek demonstrates how a small talented team, guided by strong research and development (R&D) direction and effective collaboration, can challenge major players in the AI industry. This is evident through their series of research publications, from DeepSeekMoE to the latest version, DeepSeekV3. In this post, we’ll explore the key innovations behind these publications that have contributed to DeepSeek’s success.

R&D Evolution

DeepSeek’s success didn’t happen overnight. It is the result of tackling a series of challenging research questions and the relentless efforts of a talented, hard-working team. Figure 1 provides an overview of the R&D evolution that has shaped DeepSeek into what it is today.

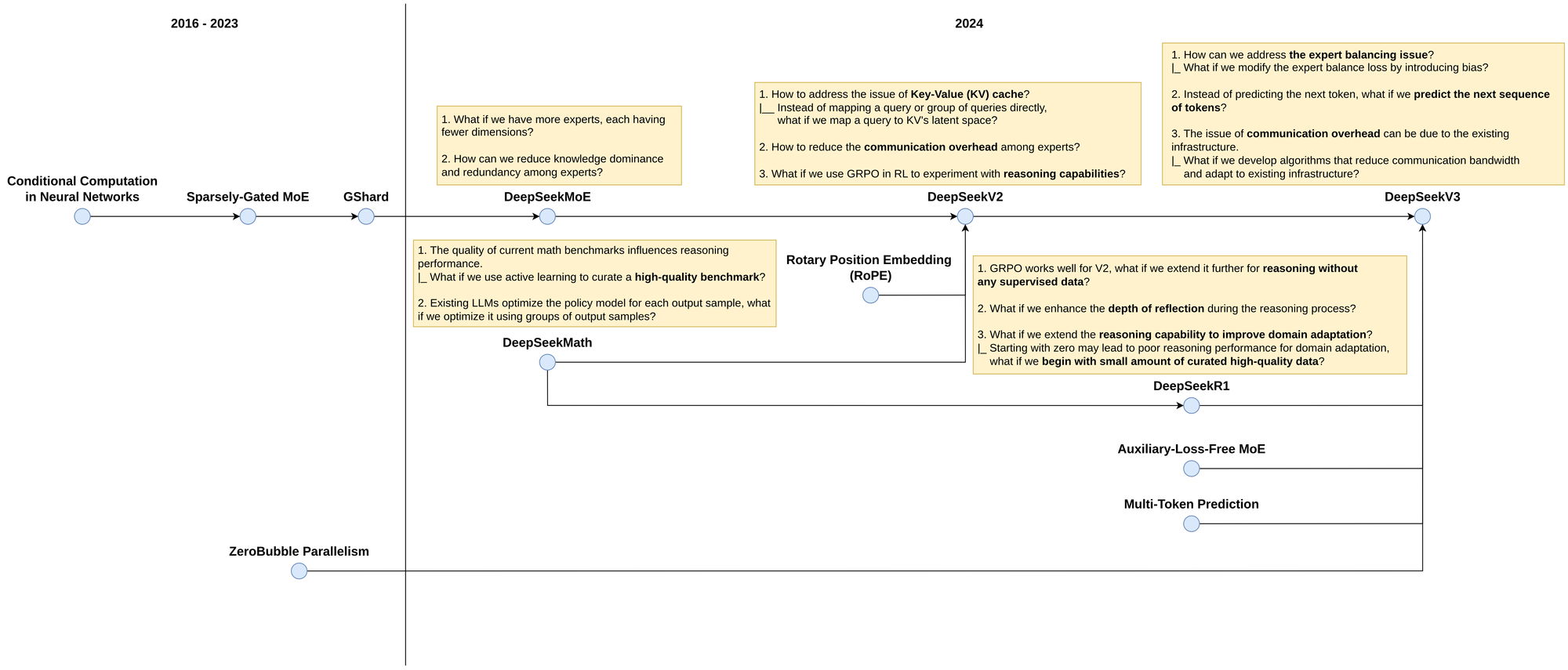
DeepSeekMoE

Mixture of Experts (MoE) [1, 2] is a machine learning architecture that uses a gating mechanism to assign tasks to specialized sub-models, or "experts," based on input data. This selective activation improves efficiency by activating only a subset of experts during inference, reducing computational costs while maintaining high performance. Specifically, a basic MoE can be formulated as:
$$y = \sum_{i=1}^{M} g_i(x) \cdot f_i(x)$$
where,

• \(y\) is the output of the MoE model.
• \(M\) is the total number of experts.
• \(g_i(x)\) is the gating function, which determines the weight or probability of using the \(i\)-th expert based on the input \(x\).
• \(f_i(x)\) is the output of the \(i\)-th expert given the input \(x\).

Mixture of Experts (MoE) is also known as a neural network mechanism that utilizes conditional computation. However, it faces algorithmic and performance challenges. To improve computational efficiency on GPU clusters, Shazeer et al. [3] introduced the sparsely-gated MoE, building upon the work of Bengio et al. [4]. Their approach reduces computation by leveraging the sparsity of the output of \(g_i(x)\). In addition, they employed both data parallelism and model parallelism to enhance data efficiency for each expert. To further scale large models using conditional computation and distributed computing, Lepikhin et al. [5] introduced GShard. This approach builds on the data and model parallelism in [3] by designing operators for matrix multiplication across multiple devices and incorporating an expert grouping mechanism to distribute the workload across these devices.

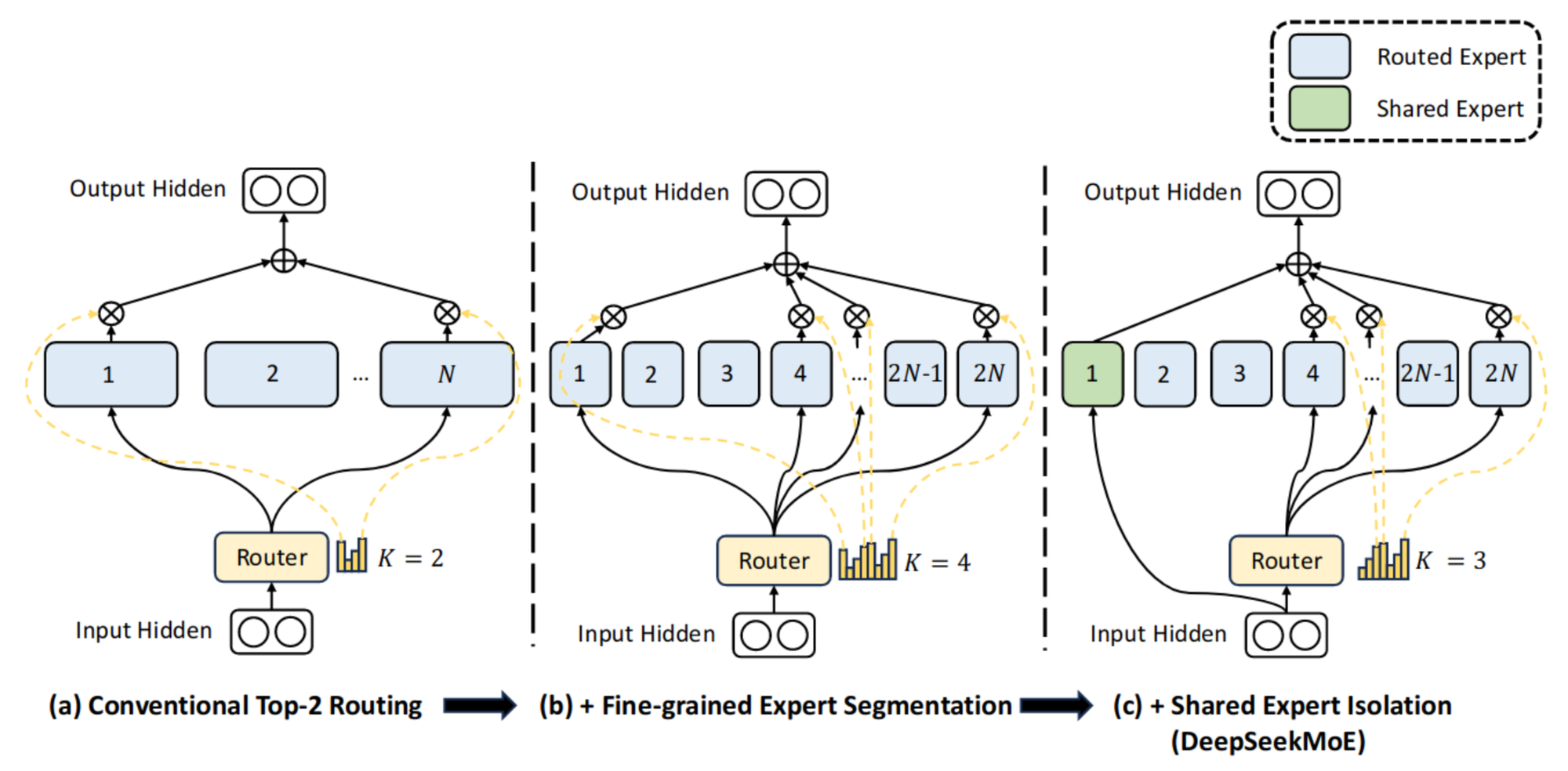
While GShard focuses on scaling large models through engineering techniques, it still faces two fundamental challenges in MoE architecture: (i) the number of latent dimensions per expert, and (ii) the knowledge dominance and redundancy among experts. To tackle the first challenge, DeepSeekMoE [6] reduces the latent dimensions for each expert while increasing the number of experts. For instance, instead of using 8 experts with 512 dimensions each across 8 devices, we can utilize 16 experts with 256 dimensions each across 16 devices. To address the second challenge, DeepSeekMoE introduces two types of experts: a shared expert, which learns from all the data, and a routed expert, which specializes in learning specific aspects of the data. Figure 2 illustrates the innovation of DeepSeekMoE.

DeepSeekMath

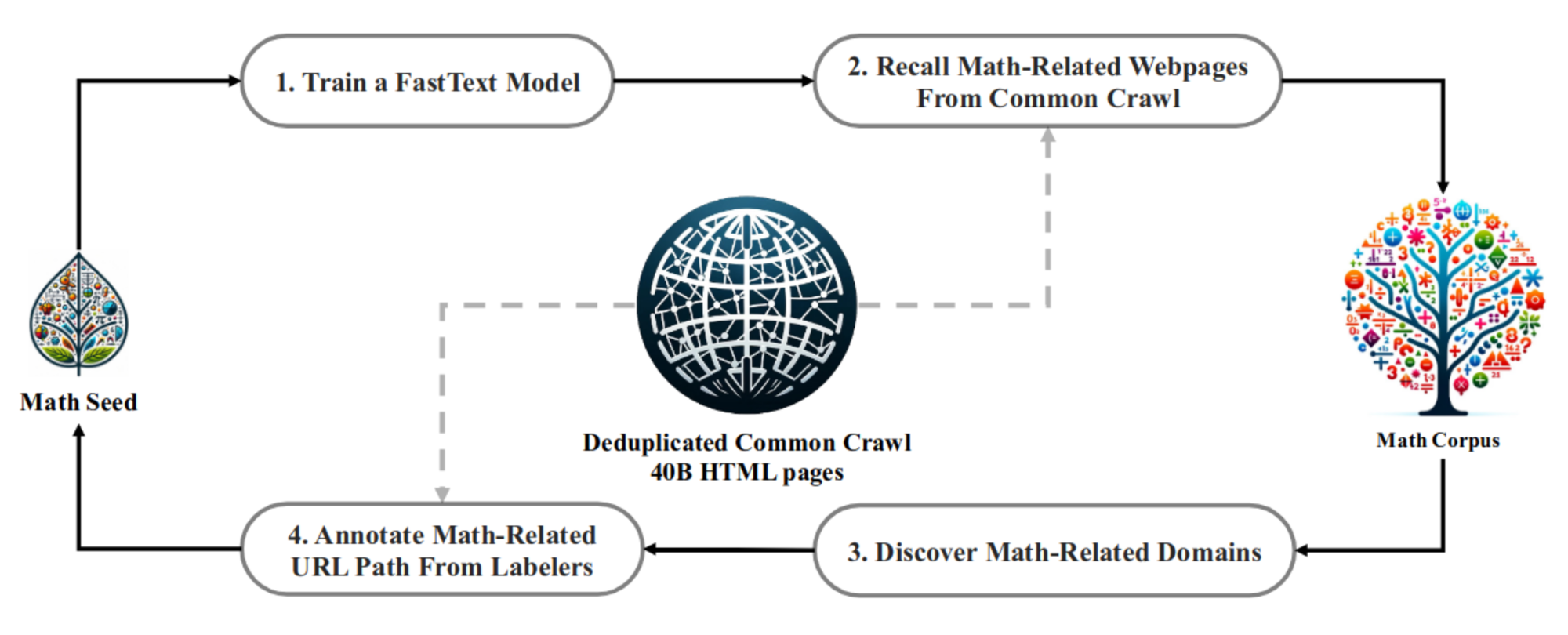
Reasoning capabilities remain a significant challenge for large language models (LLMs), often due to factors such as the lack of high-quality benchmarks for reasoning and the absence of effective reasoning mechanisms. As DeepSeekMoE is an LLM, it must be equipped with reasoning abilities to gain advantages on the market. To accomplish this, DeepSeek conducted experiments alongside DeepSeekMath [7]. To tackle the issue of high-quality reasoning benchmarks, DeepSeekMath crawls data from Common Crawl and employs active learning with minimal human intervention to curate a high-quality benchmark for mathematical reasoning (see Figure 3).

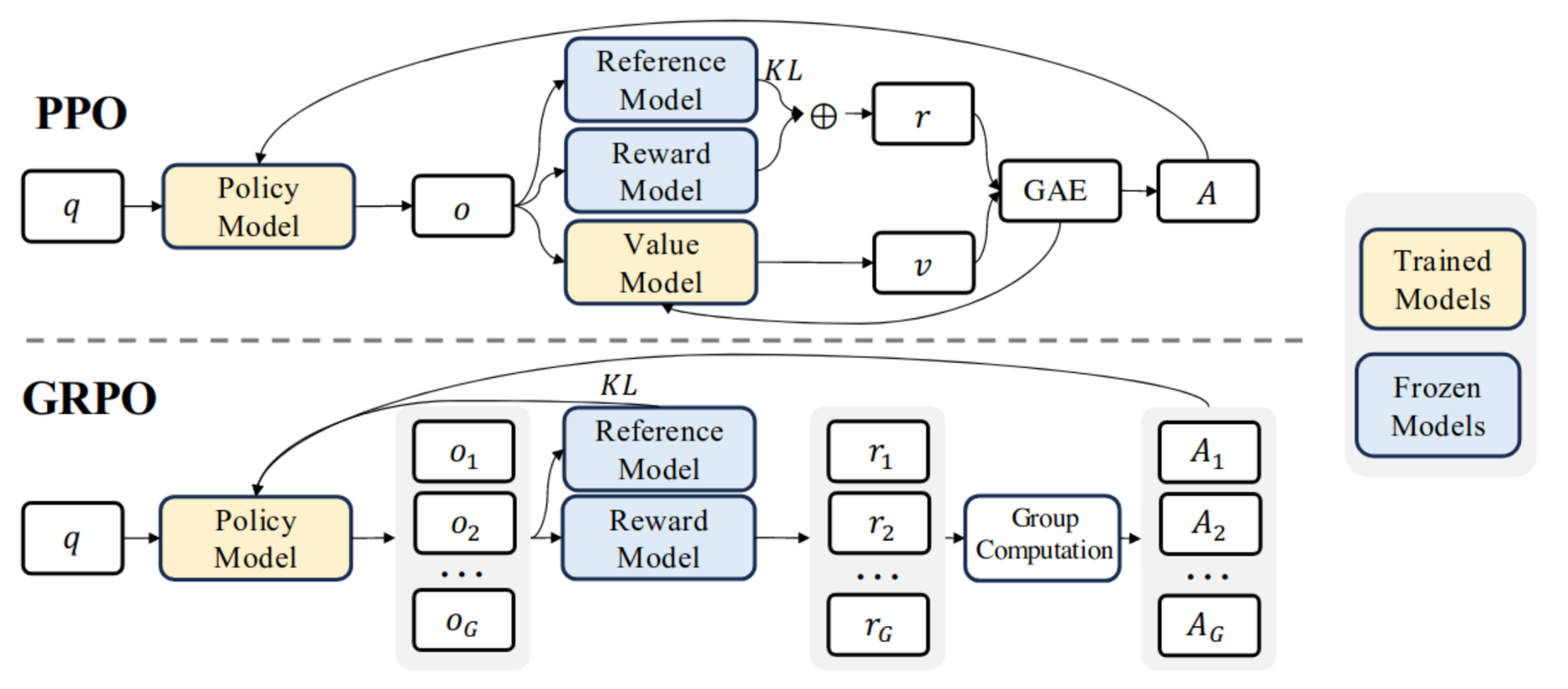
Existing LLMs use Proximal Policy Optimization (PPO) [8] or its variants for optimization and reasoning tasks. This method optimizes a policy model by assigning a single output to each state. However, for a given state, there can be multiple possible outputs. For example, the sentence "I walk in a park with my [blank]" could have various tokens to fill the blank, such as "friends," "dog," "cat," or "colleagues." Instead of relying on the traditional approach, DeepSeekMath introduces Group Relative Policy Optimization (GRPO) (see also Figure 4), which enhances PPO by optimizing a policy model using a group of outputs. In addition, this approach eliminates the value model to reduce CPU/GPU memory usage and improve computational performance.

DeepSeekV2

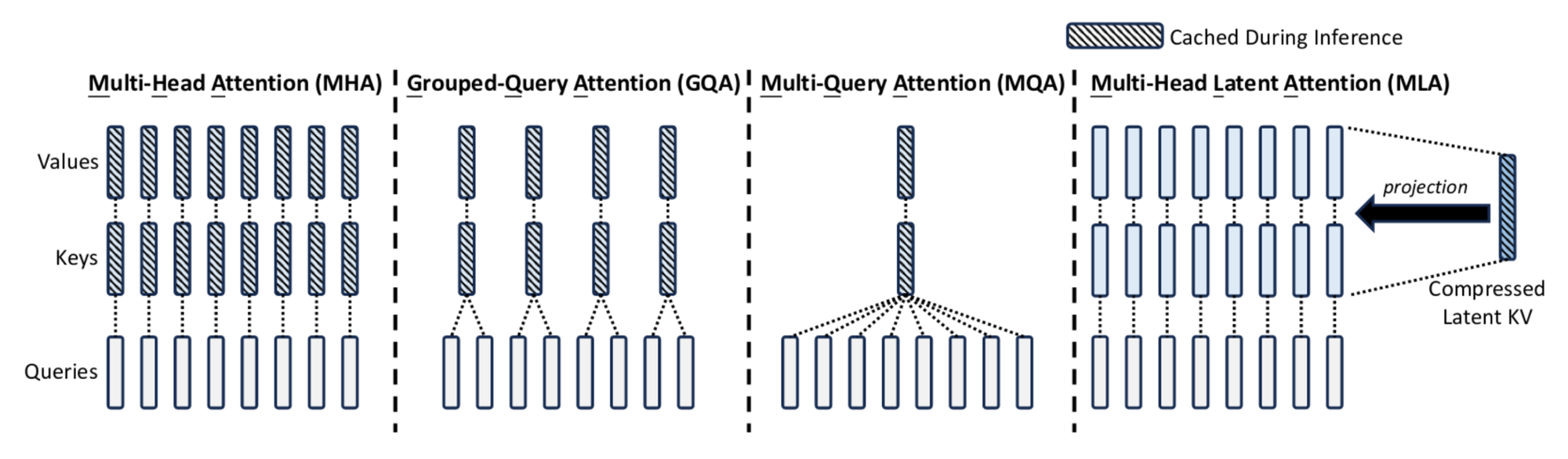
While DeepSeekMoE focuses on tackling two fundamental challenges in MoE architecture, the issue of the Key-Value (KV) cache in Transformer-based architectures persists, leading to inefficiencies during test-time inference. To overcome this, DeepSeekV2 [9] introduces Multi-Head Latent Attention (MLA), which maps a query to the compression of the KV in the latent space, rather than directly mapping a query or a group of queries to keys and values (see Figure 5). Furthermore, incorporating Rotary Position Embedding (RoPE) [10] to contextualize tokens according to their positions is a minor enhancement in DeepSeekV2.

The increase in the number of experts in DeepSeekMoE leads to the challenge of communication overhead between experts. To resolve this, DeepSeekV2 introduces a communication balance loss that ensures balanced multi-turn communication across devices.

Building on the success of GRPO in DeepSeekMath, GRPO is further integrated into DeepSeekV2. This integration aims to explore the optimization and reasoning capabilities of GRPO in domains beyond mathematics.

DeepSeekR1

GRPO demonstrates its reasoning capabilities with supervised data in both DeepSeekMath and DeepSeekV2. To further evaluate its potential in self-supervised reasoning, DeepSeekR1 [11] integrates a thinking framework similar to Chain of Thought [12] and self-reflection [13, 14] into the training process. This framework requires the model to refine its response over a set number of iterations before producing a final answer.

As the depth of thinking increases, reasoning performance improves, but computational runtime also rises. To balance reasoning accuracy and efficiency, DeepSeekR1 is fine-tuned using a small set of curated high-quality reasoning data. This success further inspires a series of experiments exploring DeepSeekR1's potential in enhancing the distillation process.

DeepSeekV3

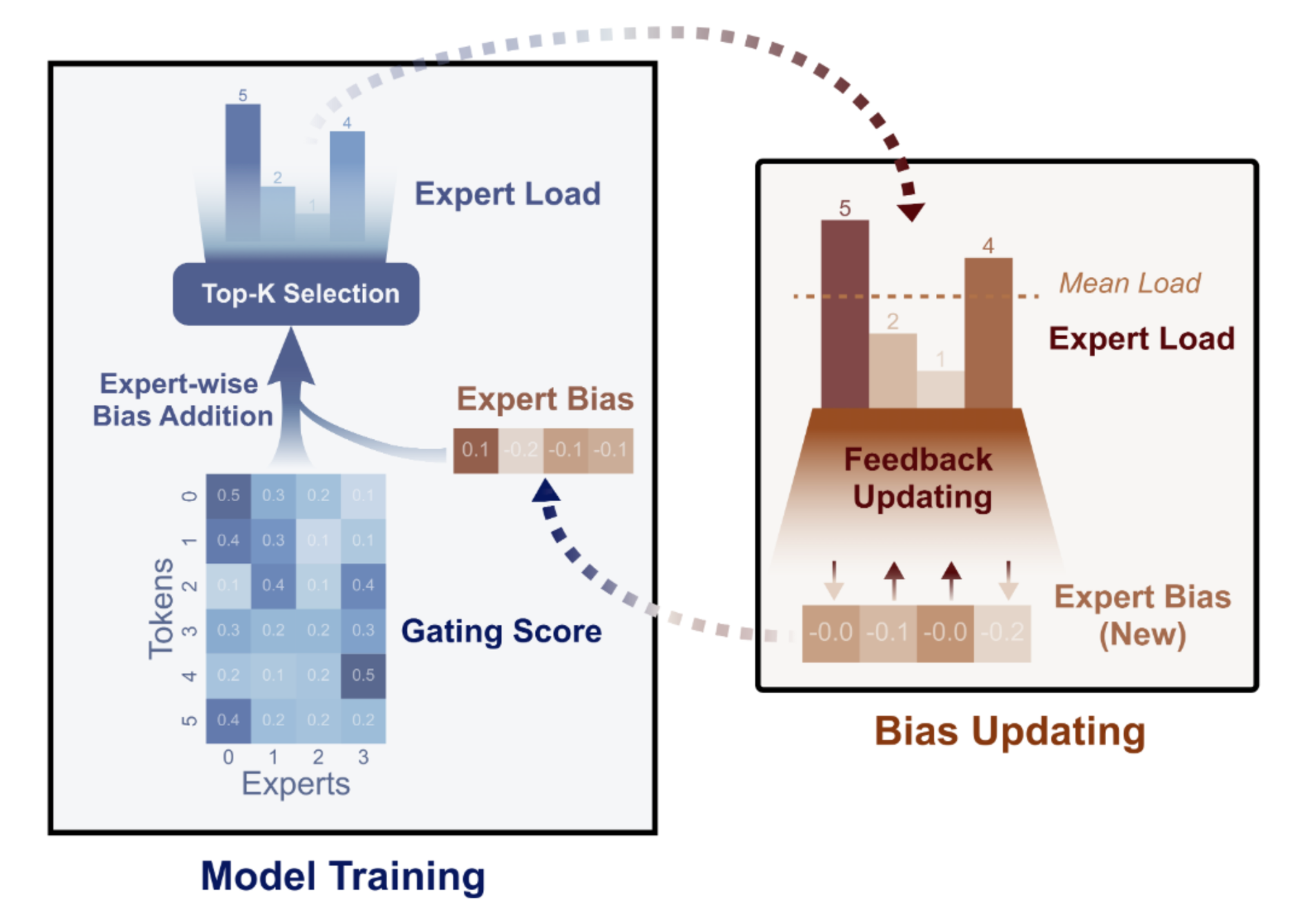
DeepSeekV2 faces the challenge of unbalanced expert load, where the gating function favors a few experts rather than distributing workload evenly. To resolve this, DeepSeekV3 [15] replaces the expert balance loss [5] with an auxiliary-loss-free load balancing strategy [16]. This approach incorporates expert bias into the gating function and reinforces it through feedback (see Figure 6).

To further improve overall performance, DeepSeekV3 utilizes the multi-token prediction (MTP) capability from [17] to predict the next sequence of tokens. Additionally, this enhances data efficiency and optimizes the planning process for generating more effective representations.

Despite advancements, communication overhead remains a challenge due to limitations in existing computational infrastructure. To tackle this, DeepSeekV3 incorporates ZeroBubble [18], a scheduling strategy that enhances synchronization between training pipelines. Building on this, it introduces a novel pipeline parallelism algorithm called DualPipe, designed to help DeepSeekV3 adapt to current computational infrastructure and reduce communication overhead.

References

1. Jacobs, R.A., Jordan, M.I., Nowlan, S.J. and Hinton, G.E., 1991. Adaptive mixtures of local experts. Neural computation, 3(1), pp.79-87.
2. Jordan, M.I. and Jacobs, R.A., 1994. Hierarchical mixtures of experts and the EM algorithm. Neural computation, 6(2), pp.181-214.
3. Shazeer, N., Mirhoseini, A., Maziarz, K., Davis, A., Le, Q., Hinton, G. and Dean, J., 2017. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. arXiv preprint arXiv:1701.06538.
4. Bengio, E., Bacon, P.L., Pineau, J. and Precup, D., 2015. Conditional computation in neural networks for faster models. arXiv preprint arXiv:1511.06297.
5. Lepikhin, D., Lee, H., Xu, Y., Chen, D., Firat, O., Huang, Y., Krikun, M., Shazeer, N. and Chen, Z., 2020. Gshard: Scaling giant models with conditional computation and automatic sharding. arXiv preprint arXiv:2006.16668.
6. Dai, D., Deng, C., Zhao, C., Xu, R.X., Gao, H., Chen, D., Li, J., Zeng, W., Yu, X., Wu, Y. and Xie, Z., 2024. Deepseekmoe: Towards ultimate expert specialization in mixture-of-experts language models. arXiv preprint arXiv:2401.06066.
7. Shao, Z., Wang, P., Zhu, Q., Xu, R., Song, J., Bi, X., Zhang, H., Zhang, M., Li, Y.K., Wu, Y. and Guo, D., 2024. Deepseekmath: Pushing the limits of mathematical reasoning in open language models. arXiv preprint arXiv:2402.03300.
8. Schulman, J., Wolski, F., Dhariwal, P., Radford, A. and Klimov, O., 2017. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347.
9. Liu, A., Feng, B., Wang, B., Wang, B., Liu, B., Zhao, C., Dengr, C., Ruan, C., Dai, D., Guo, D. and Yang, D., 2024. Deepseek-v2: A strong, economical, and efficient mixture-of-experts language model. arXiv preprint arXiv:2405.04434.
10. Su, J., Ahmed, M., Lu, Y., Pan, S., Bo, W. and Liu, Y., 2024. Roformer: Enhanced transformer with rotary position embedding. Neurocomputing, 568, p.127063.
11. Guo, D., Yang, D., Zhang, H., Song, J., Zhang, R., Xu, R., Zhu, Q., Ma, S., Wang, P., Bi, X. and Zhang, X., 2025. Deepseek-r1: Incentivizing reasoning capability in llms via reinforcement learning. arXiv preprint arXiv:2501.12948.
12. Wei, J., Wang, X., Schuurmans, D., Bosma, M., Xia, F., Chi, E., Le, Q.V. and Zhou, D., 2022. Chain-of-thought prompting elicits reasoning in large language models. Advances in neural information processing systems, 35, pp.24824-24837.
13. Ji, Z., Yu, T., Xu, Y., Lee, N., Ishii, E. and Fung, P., 2023, December. Towards mitigating LLM hallucination via self reflection. In Findings of the Association for Computational Linguistics: EMNLP 2023 (pp. 1827-1843).
14. Madaan, A., Tandon, N., Gupta, P., Hallinan, S., Gao, L., Wiegreffe, S., Alon, U., Dziri, N., Prabhumoye, S., Yang, Y. and Gupta, S., 2024. Self-refine: Iterative refinement with self-feedback. Advances in Neural Information Processing Systems, 36.
15. Liu, A., Feng, B., Xue, B., Wang, B., Wu, B., Lu, C., Zhao, C., Deng, C., Zhang, C., Ruan, C. and Dai, D., 2024. Deepseek-v3 technical report. arXiv preprint arXiv:2412.19437.
16. Wang, L., Gao, H., Zhao, C., Sun, X. and Dai, D., 2024. Auxiliary-loss-free load balancing strategy for mixture-of-experts. arXiv preprint arXiv:2408.15664.
17. Gloeckle, F., Idrissi, B.Y., Rozière, B., Lopez-Paz, D. and Synnaeve, G., 2024. Better & faster large language models via multi-token prediction. arXiv preprint arXiv:2404.19737.
18. Qi, P., Wan, X., Huang, G. and Lin, M., 2023. Zero bubble pipeline parallelism. arXiv preprint arXiv:2401.10241.